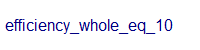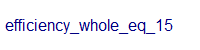Purely as an example, suppose we have a series of 10 MVRs over 10 years starting at 1.88% and ending at 9.29% accompanied by10 DVRs over 10 years starting at 2.60% and ending at 9.82% (figures shown below). For simplicity, I have random numbers which are monotonically increasing but that certainly won’t always be the case. The measures are for 1 year, over 2 years … ending up over the whole 10 years. We need to focus upon the MVR endpoint of 9.29%.

Are the DVR’s overall nearer to the MVR endpoint than the DVRs? Dividing all of the numbers by the MVR endpoint, we can compare the ratios with one. Drawing the curves for this simple case, one can see that the DVRs (red) are much closer than the MVRs (blue). No, this won’t always be the case! To assess what I’ve called efficiency, I think it reasonable to calculate the ratio of the absolute area between red and grey divided by the absolute area between blue and grey. If below 1, then that ratio indicates that DVRs were a better predictor of the MVR endpoint.

For periods of 10 years or 15 years, static charts show the efficiency for equities by start year. An interactive chart shows the same data by start year (upper slider) for sub-periods of between 10 years and 15 years (lower slider). This can be toggled by asset category. Start year plus period cannot exceed 2022.